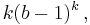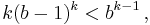Narcissistic number

In recreational number theory, a narcissistic number^[1]^[2] (also known as a pluperfect digital invariant (PPDI),^[3] an Armstrong number^[4] (after Michael F. Armstrong)^[5] or a plus perfect number)^[6] is a number that is the sum of its own digits each raised to the power of the number of digits. This definition depends on the base b of the number system used, e.g. b = 10 for the decimal system or b = 2 for the binary system.

The definition of a narcissistic number relies on the decimal representation n = d_kd_k-1...d₁d₀ of a natural number n, e.g.

n = d_k·10^k-1 + d_k-1·10^k-2 + ... + d₂·10 + d₁,

with k digits d_i satisfying 0 ≤ d_i ≤ 9. Such a number n is called narcissistic if it satisfies the condition

n = d_k^k + d_k-1^k + ... + d₂^k + d₁^k.

For example the 3-digit decimal number 153 is a narcissistic number because 153 = 1³ + 5³ + 3³.

Narcissistic numbers can also be defined with respect to numeral systems with a base b other than b = 10. The base-b representation of a natural number n is defined by

n = d_kb^k-1 + d_k-1b^k-2 + ... + d₂b + d₁,

where the base-b digits d_i satisfy the condition 0 ≤ d_i ≤ b-1. For example the (decimal) number 17 is a narcissistic number with respect to the numeral system with base b = 3. Its three base-3 digits are 122, because 17 = 1·3² + 2·3 + 2 , and it satisfies the equation 17 = 1³ + 2³ + 2³.

If the constraint that the power must equal the number of digits is dropped, so that for some m possibly different from k it happens that

n = d_k^m + d_k-1^m + ... + d₂^m + d₁^m,

then n is called a perfect digital invariant or PDI.^[7]^[2] For example, the decimal number 4150 has four decimal digits and is the sum of the fifth powers of its decimal digits

4150 = 4⁵ + 1⁵ + 5⁵ + 0⁵,

so it is a perfect digital invariant but not a narcissistic number.

In "A Mathematician's Apology", G. H. Hardy wrote:

There are just four numbers, after unity, which are the sums of the cubes of their digits:

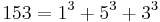
$153=1^3%2B5^3%2B3^3$

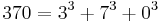
$370=3^3%2B7^3%2B0^3$

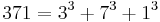
$371=3^3%2B7^3%2B1^3$

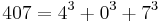$407=4^3%2B0^3%2B7^3$ .

These are odd facts, very suitable for puzzle columns and likely to amuse amateurs, but there is nothing in them which appeals to the mathematician.

1 Narcissistic numbers in various bases
2 Related concepts
3 References
4 External links

Narcissistic numbers in various bases

The sequence of "base 10" narcissistic numbers starts: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1634, 8208, 9474 ... (sequence A005188 in OEIS)

The sequence of "base 3" narcissistic numbers starts: 0, 1, 2, 12, 122

The sequence of "base 4" narcissistic numbers starts: 0, 1, 2, 3, 313

The number of narcissistic numbers in a given base is finite, since the maximum possible sum of the kth powers of a k digit number in base b is

$k(b-1)^k\, ,$

and if k is large enough then

$k(b-1)^k<b^{k-1}\, ,$

in which case no base b narcissistic number can have k or more digits.

There are 88 narcissistic numbers in base 10, of which the largest is

115,132,219,018,763,992,565,095,597,973,971,522,401

with 39 digits.^[1]

Unlike narcissistic numbers, no upper bound can be determined for the size of PDIs in a given base, and it is not currently known whether or not the number of PDIs for an arbitrary base is finite or infinite.^[2]

Related concepts

The term "narcissistic number" is sometimes used in a wider sense to mean a number that is equal to any mathematical manipulation of its own digits. With this wider definition narcisstic numbers include:

Constant base numbers : 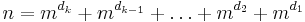$n=m^{d_k} %2B m^{d_{k-1}} %2B \dots %2B m^{d_2} %2B m^{d_1}$ for some m.
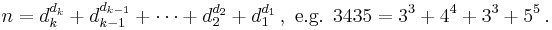
Perfect digit-to-digit invariants (sequence A046253 in OEIS) : $n = d_k^{d_k} %2B d_{k-1}^{d_{k-1}} %2B \dots %2B d_2^{d_2} %2B d_1^{d_1}\, ,\text{ e.g. } 3435 = 3^3 %2B 4^4 %2B 3^3 %2B 5^5\, .$
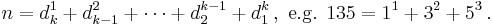
Ascending power numbers (sequence A032799 in OEIS) : $n = d_k^1 %2B d_{k-1}^2 %2B \dots %2B d_2^{k-1} %2B d_1^k\, ,\text{ e.g. } 135 = 1^1 %2B 3^2 %2B 5^3 \, .$
Friedman numbers (sequence A036057 in OEIS).
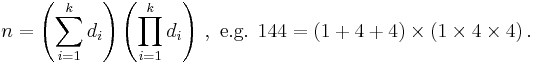
Sum-product numbers (sequence A038369 in OEIS) : $n=\left(\sum_{i=1}^{k}{d_i}\right) \left(\prod_{i=1}^{k}{d_i}\right) \, ,\text{ e.g. } 144 = (1%2B4%2B4) \times (1 \times4 \times 4) \, .$
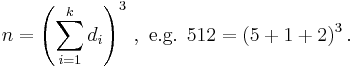
Dudeney numbers (sequence A061209 in OEIS) : $n=\left(\sum_{i=1}^{k}{d_i}\right)^3\, ,\text{ e.g. } 512 = (5%2B1%2B2)^3 \, .$
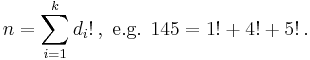
Factorions (sequence A014080 in OEIS) : $n=\sum_{i=1}^{k}{d_i}!\, ,\text{ e.g. } 145 = 1! %2B 4! %2B 5! \, .$

where d_i are the digits of n in some base.

References

^ ^a ^b Weisstein, Eric W., "Narcissistic Number" from MathWorld.
^ ^a ^b ^c Perfect and PluPerfect Digital Invariants by Scott Moore
^ PPDI (Armstrong) Numbers by Harvey Heinz
^ Armstrong Numbersl by Dik T. Winter
^ Lionel Deimel’s Web Log
^ (sequence A005188 in OEIS)
^ PDIs by Harvey Heinz

Joseph S. Madachy, Mathematics on Vacation, Thomas Nelson & Sons Ltd. 1966, pages 163-175.
Perfect Digital Invariants by Walter Schneider
On a curious property of 3435 by Daan van Berkel

Narcissistic number

Contents

Narcissistic numbers in various bases

Related concepts

References

External links